SVM (1)
\begin{align} \newcommand{\cS}{\mathcal{S}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bphi}{\boldsymbol{\phi}} \newcommand{\balpha}{\boldsymbol{\alpha}} \newcommand{\bSigma}{\boldsymbol{\Sigma}} \nonumber \end{align}
SVMを復習しよう.今回は最も基本的なケースであるハードマージンかつ線形のSVMについて書く.これは2クラス分類問題において,ある線形判別関数$g(\bx)$によって線形分離可能であることを仮定している. ハードマージンSVMの詳細については後で更新が確認しやすいように,ブログとは別のこちらのページに書いてあるので,まずはそちらを見て頂きたい.
CVXOPTによる実装例
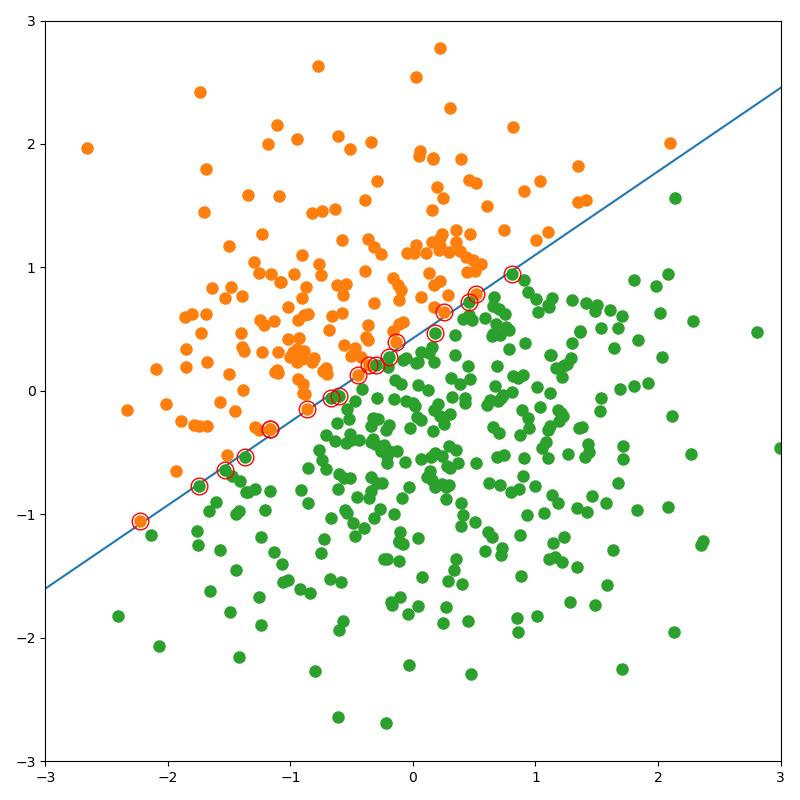
凸最適化のためのパッケージCVXOPTで$\balpha$を求めてみよう.以下,コードと実行結果の例である.赤丸で囲んでいるサンプルは$\alpha_i > 0$,即ちサポートベクトルに対応するサンプルである.