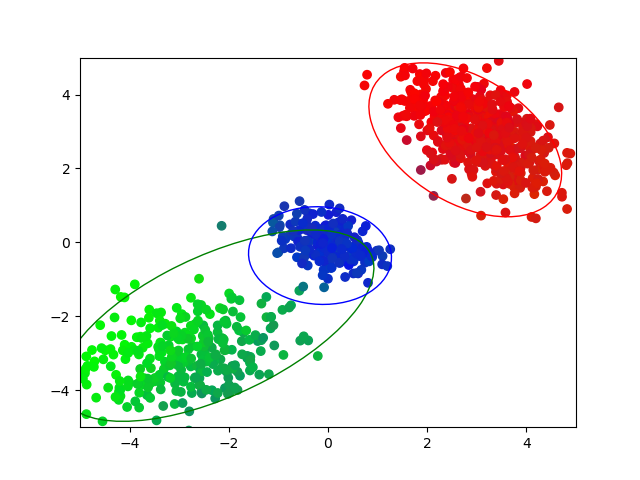
ガウス混合モデルでギブスサンプリング
\begin{align} \newcommand{\b}[1]{\mathbf{#1}} \newcommand{\bo}[1]{\boldsymbol{#1}} \nonumber \end{align}
ベイズ推論による機械学習入門より,ガウス混合モデルでギブスサンプリングをしてみます.
記号の表記は以下の通りです.
- クラスタの数$K$
- クラスタの混合比率$\bo{\pi}$
- クラスタの割り当て$\b{s}_n$
- クラスタ$k$のパラメータ$\bo{\theta}_k = \left\{ \bo{\mu}_k, \bo{\Lambda}_k \right\}$
- $\bo{\mu} = \left\{ \bo{\mu}_1, \ldots, \bo{\mu}_K \right\}, \bo{\Lambda} = \left\{ \bo{\Lambda}_1, \ldots, \bo{\Lambda}_K \right\}$
各クラスタ$k$に対して,データ$\b{x}_n \in \mathbb{R}^D$の観測モデルをガウス分布とします.
\begin{align} p(\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k) = \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}^{-1}) \end{align}
また事前分布として,ガウス分布の共役事前分布にあたるガウス・ウィシャート分布を用います.
\begin{align} p(\bo{\mu}_k, \bo{\Lambda}_k) = \mathcal{N} (\bo{\mu}_k | \b{m}, (\beta \bo{\Lambda}_k)^{-1}) \mathcal{W} (\bo{\Lambda}_k | \nu, \b{W}) \end{align} ここで$\b{m} \in \mathbb{R}^D, \beta \in \mathbb{R}^+, \b{W} \in \mathbb{R}^{D \times D}, \nu > D - 1$はハイパーパラメータです.
さて,ギブスサンプリングについて考えていきます.データ$\b{X} = \left\{ \b{x}_1, \ldots, \b{x}_N \right\}$が与えられたときの事後分布$p(\b{S}, \bo{\mu}, \bo{\Lambda}, \bo{\pi} | \b{X})$を考え,パラメータと潜在変数に分解してサンプリングすることにします.
\begin{align} \b{S} &\sim p(\b{S} | \b{X}, \bo{\mu}, \bo{\Lambda}, \bo{\pi}) \newline \bo{\mu}, \bo{\Lambda}, \bo{\pi} &\sim p(\bo{\mu}, \bo{\Lambda}, \bo{\pi} | \b{X}, \b{S}) \end{align}
まず,$\b{S}$をサンプルするための分布を求めます.$\b{S}$を含まない分布を無視することによって
\begin{align} p(\b{S} | \b{X}, \bo{\mu}, \bo{\Lambda}, \bo{\pi}) &\propto p(\b{S}, \b{X}, \bo{\mu}, \bo{\Lambda}, \bo{\pi}) \newline &= p(\b{S} | \bo{\pi}) p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) p(\bo{\mu}, \bo{\Lambda}) p(\bo{\pi}) \newline &\propto p(\b{S} | \bo{\pi}) p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) \newline &= \prod_{n = 1}^N p(\b{x}_n | \b{s}_n, \bo{\mu}, \bo{\Lambda}) p (\b{s}_n | \bo{\pi}) \end{align}
となります.対数をとって各分布を変形していきます.
\begin{align} \ln p(\b{x}_n | \b{s}_n, \bo{\mu}, \bo{\Lambda}) &= \sum_{k = 1}^K s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) \newline &= \sum_{k = 1}^K s_{n, k} \left[ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| \right] + \mathrm{const.} \newline \ln p(\b{s}_n | \bo{\pi}) &= \ln \mathrm{Cat} (\b{s}_n | \bo{\pi}) = \sum_{k = 1}^K s_{n, k} \ln \pi_k \end{align}
よって
\begin{align} \ln p(\b{x}_n | \b{s}_n, \bo{\mu}, \bo{\Lambda}) p(\b{s}_n | \bo{\pi}) &= \sum_{k = 1}^K s_{n, k} \left[ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| + \ln \pi_k \right] + \mathrm{const.} \end{align}
\begin{align} \b{s}_n \sim \mathrm{Cat} (\b{s}_n | \bo{\eta}_n) \end{align}
\begin{align} \eta_{n, k} \propto \exp \left[ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| + \ln \pi_k \right] \quad \left( \mathrm{s.t.} \quad \sum_{k = 1}^K \eta_{n, k} = 1 \right) \end{align}
となります.ここまでは易しいのですが,ここからが結構大変です. 次はパラメータ$\bo{\mu}, \bo{\Lambda}, \bo{\pi}$をサンプルするための分布を求めます.
\begin{align} p(\bo{\mu}, \bo{\Lambda}, \bo{\pi} | \b{X}, \b{S}) &\propto p(\b{X}, \b{S}, \bo{\mu}, \bo{\Lambda}, \bo{\pi}) \newline &= p(\b{S} | \bo{\pi}) p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) p(\bo{\mu}, \bo{\Lambda}) p(\bo{\pi}) \end{align}
ここから$\bo{\mu}, \bo{\Lambda}$の分布と$\bo{\pi}$の分布に分解できることが分かります. まず,$\bo{\mu}, \bo{\Lambda}$の分布について考えていきます.
\begin{align} \ln p(\b{X} | \bo{\mu}, \bo{\Lambda}, \b{S}) p(\bo{\mu}, \bo{\Lambda}) &= \sum_{n = 1}^N \sum_{k = 1}^K s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \sum_{k = 1}^K \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) \newline &= \sum_{k = 1}^K \left\{ \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) \right\} \end{align}
上記の式から,求めたい分布は独立な$K$個の分布に分解できることが分かります. ここで,ある$k$について$p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S}) = p(\bo{\mu}_k | \bo{\Lambda}_k, \b{X}, \b{S}) p(\bo{\Lambda}_k | \b{X}, \b{S})$と変形できることを利用します. $k$に関する和の中身を$\bo{\mu}_k$に関して整理すると($\bo{\mu}_k$を含まない項を定数とみなすと)
\begin{align} & \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) \newline &= \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathcal{N} (\bo{\mu}_k | \b{m}, (\beta \bo{\Lambda}_k)^{-1}) + \ln \mathcal{W} (\bo{\Lambda}_k | \nu, \b{W}) \newline &= \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathcal{N} (\bo{\mu}_k | \b{m}, (\beta \bo{\Lambda}_k)^{-1}) + \mathrm{const.} \newline &= \sum_{n = 1}^N s_{n, k} \left[ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) \right] + \left[ - \frac{1}{2} (\bo{\mu}_k - \b{m})^T \beta \bo{\Lambda}_k (\bo{\mu}_k - \b{m}) \right] + \mathrm{const.} \newline &= - \frac{1}{2} \sum_{n = 1}^N s_{n, k} \left[ - 2 \bo{\mu}_k^T \bo{\Lambda}_k \b{x}_n + \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k \right] - \frac{1}{2} \left[ - 2 \bo{\mu}_k^T \beta \bo{\Lambda}_k \b{m} + \bo{\mu}_k^T \beta \bo{\Lambda}_k \b{m} \right] + \mathrm{const.} \newline &= - \frac{1}{2} \left[ \bo{\mu}_k^T \left( \sum_{n = 1}^N s_{n, k} + \beta \right) \bo{\Lambda}_k \bo{\mu}_k - 2 \bo{\mu}_k^T \left( \bo{\Lambda}_k \sum_{n = 1}^N s_{n, k} \b{x}_n + \beta \bo{\Lambda}_k \b{m} \right) \right] + \mathrm{const.} \end{align}
となります.したがって$\bo{\mu}_k$はガウス分布で
\begin{align} \bo{\mu}_k \sim \mathcal{N} (\bo{\mu}_k | \hat{\b{m}}_k, (\hat{\beta}_k \bo{\Lambda}_k)^{-1}) \end{align}
$\hat{\beta}_k, \hat{\b{m}}_k$は
\begin{align} \hat{\beta}_k &= \sum_{n = 1}^N s_{n, k} + \beta \newline \hat{\b{m}}_k &= \frac{\sum_{n = 1}^N s_{n, k} \b{x}_n + \beta \b{m}}{\hat{\beta}_k} \quad \left( \hat{\beta}_k \bo{\Lambda}_k \hat{\b{m}}_k = \bo{\Lambda}_k \sum_{n = 1}^N s_{n, k} \b{x}_n + \beta \bo{\Lambda}_k \b{m} \text{より} \right) \end{align}
となります.
$p(\bo{\mu}_k | \bo{\Lambda}_k, \b{X}, \b{S})$が求められれば,
\begin{align} \ln p(\bo{\Lambda}_k | \b{X}, \b{S}) = \ln p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S}) - \ln p(\bo{\mu}_k | \bo{\Lambda}_k, \b{X}, \b{S}) \end{align}
から$\bo{\Lambda}_k$についての式を得ることができます.ここで$\ln p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S})$は次のように求めます.$p(\bo{\mu}, \bo{\Lambda} | \b{X}, \b{S})$を変形すると
\begin{align} p(\bo{\mu}, \bo{\Lambda} | \b{X}, \b{S}) &\propto p(\b{X}, \b{S}, \bo{\mu}, \bo{\Lambda}) \newline &= p(\b{X} | \bo{\mu}, \bo{\Lambda}, \b{S}) p(\bo{\mu}, \bo{\Lambda} | \b{S}) p(\b{S}) \newline &= p(\b{X} | \bo{\mu}, \bo{\Lambda}, \b{S}) p(\bo{\mu}, \bo{\Lambda}) p(\b{S}) \newline &\propto p(\b{X} | \bo{\mu}, \bo{\Lambda}, \b{S}) p(\bo{\mu}, \bo{\Lambda}) \end{align}
となります.この分布の対数は既に出てきており,
\begin{align} \ln p(\b{X} | \bo{\mu}, \bo{\Lambda}, \b{S}) p(\bo{\mu}, \bo{\Lambda}) &= \sum_{k = 1}^K \left\{ \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) \right\} \end{align}
でした.これは$K$個の独立な分布に分解できるということだったので,$k$に対応する$\ln p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S})$は
\begin{align} \ln p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S}) = \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) + \mathrm{const.} \end{align}
ということになります.以上の結果から,$\bo{\Lambda}_k$について整理します.ここで$ \ln | \beta \bo{\Lambda}_k | = \ln \beta^D | \bo{\Lambda}_k | = \ln \beta^D + \ln | \bo{\Lambda}_k | = \ln | \bo{\Lambda}_k | + \mathrm{const.}$となることを途中で用います.
\begin{align} & \ln p(\bo{\Lambda}_k | \b{X}, \b{S}) \newline &= \ln p(\bo{\mu}_k, \bo{\Lambda}_k | \b{X}, \b{S}) - \ln p(\bo{\mu}_k | \bo{\Lambda}_k, \b{X}, \b{S}) \newline &= \sum_{n = 1}^N s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) - \ln \mathcal{N} (\bo{\mu}_k | \hat{\b{m}}_k, (\hat{\beta}_k \bo{\Lambda}_k)^{-1}) + \mathrm{const.} \newline &= \sum_{n = 1}^N s_{n, k} \left\{ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| \right\} + \left\{ - \frac{1}{2} (\bo{\mu}_k - \b{m})^T \beta \bo{\Lambda}_k (\bo{\mu}_k -\b{m}) + \frac{1}{2} \ln |\beta \bo{\Lambda}_k| \right\} \newline &+ \frac{\nu - D - 1}{2} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} (\b{W}^{-1} \bo{\Lambda}_k) - \left\{ - \frac{1}{2} (\bo{\mu}_k - \hat{\b{m}}_k)^T \hat{\beta}_k \bo{\Lambda}_k (\bo{\mu}_k - \hat{\b{m}}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| \right\} + \mathrm{const.} \newline &= - \frac{1}{2} \sum_{n = 1}^N s_{n, k} \b{x}_n^T \bo{\Lambda}_k \b{x}_n + \frac{1}{2} \sum_{n = 1}^N s_{n, k} \ln |\bo{\Lambda}_k| - \frac{1}{2} \b{m}^T \beta \bo{\Lambda}_k \b{m} + \frac{1}{2} \ln |\bo{\Lambda}_k| \newline &+ \frac{\nu - D - 1}{2} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} (\b{W}^{-1} \bo{\Lambda}_k) + \frac{1}{2} \hat{\b{m}}_k^T \hat{\beta}_k\bo{\Lambda}_k \hat{\b{m}}_k - \frac{1}{2} \ln |\bo{\Lambda}_k| + \mathrm{const.} \newline &= - \frac{1}{2} \sum_{n = 1}^N s_{n, k} \mathrm{Tr} (\b{x}_n \b{x}_n^T \bo{\Lambda}_k) + \frac{1}{2} \sum_{n = 1}^N s_{n, k} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} (\beta \b{m} \b{m}^T \bo{\Lambda}_k) \newline &+ \frac{\nu - D - 1}{2} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} (\b{W}^{-1} \bo{\Lambda}_k) + \frac{1}{2} \mathrm{Tr} (\hat{\beta}_k \hat{\b{m}}_k \hat{\b{m}}_k^T \bo{\Lambda}_k) + \mathrm{const.} \newline &= \frac{\sum_{n = 1}^N s_{n, k} + \nu - D - 1}{2} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} \left[ \left( \sum_{n = 1}^N s_{n, k} \b{x}_n \b{x}_n^T + \beta \b{m} \b{m}^T - \hat{\beta}_k \hat{\b{m}}_k \hat{\b{m}}_k^T + \b{W}^{-1} \right) \bo{\Lambda}_k \right] + \mathrm{const.} \end{align}
したがってこれはウィシャート分布で
\begin{align} \bo{\Lambda}_k \sim \mathcal{W} (\bo{\Lambda}_k | \hat{\nu}_k, \hat{\b{W}}_k) \end{align}
\begin{align} \hat{\b{W}}_k^{-1} &= \sum_{n = 1}^N s_{n, k} \b{x}_n \b{x}_n^T + \beta \b{m} \b{m}^T - \hat{\beta}_k \hat{\b{m}}_k \hat{\b{m}}_k^T + \b{W}^{-1} \newline \hat{\nu}_k &= \sum_{n = 1}^N s_{n, k} + \nu \end{align}
となります.最後に$\bo{\pi}$についての分布を求めます.$p(\b{\pi} | \b{X}, \b{S}) \propto p(\b{S} | \bo{\pi}) p(\bo{\pi})$から
\begin{align} \ln p(\b{S} | \bo{\pi}) + \ln p(\bo{\pi}) &= \sum_{n = 1}^N \ln \mathrm{Cat} (\b{s}_n | \bo{\pi}) + \ln \mathrm{Dir} ( \bo{\pi} | \bo{\alpha}) \newline &= \sum_{n = 1}^N \sum_{k = 1}^K s_{n, k} \ln \pi_k + \sum_{k = 1}^K (\alpha_k - 1) \ln \pi_k + \mathrm{const.} \newline &= \sum_{k = 1}^K \left( \sum_{n = 1}^N s_{n, k} + \alpha_k - 1 \right) \ln \pi_k + \mathrm{const.} \end{align}
となるので,
\begin{align} \bo{\pi} \sim \mathrm{Dir} (\bo{\pi} | \hat{\bo{\alpha}}) \end{align}
\begin{align} \hat{\alpha}_k = \sum_{n = 1}^N s_{n, k} + \alpha_k \end{align}
です.これで必要な分布は全て求まりました.
最後に,アルゴリズムとして整理します.
- Set initial values $\bo{\mu}, \bo{\Lambda}, \bo{\pi}$.
- for $i = 1, 2, \ldots, T$ do
- for $n = 1, \ldots, N$ do
- Sample $\b{s}_n \sim \mathrm{Cat} (\b{s}_n | \bo{\eta}_n) $
- end for
- for $k = 1, \ldots, K$ do
- Sample $\bo{\Lambda}_k \sim \mathcal{W} (\bo{\Lambda}_k | \hat{\nu}_k, \hat{\b{W}}_k)$
- Sample $\bo{\mu}_k \sim \mathcal{N} (\bo{\mu}_k | \hat{\b{m}}_k, (\hat{\beta}_k \bo{\Lambda}_k)^{-1})$
- end for
- Sample $\bo{\pi} \sim \mathrm{Dir} (\bo{\pi} | \hat{\bo{\alpha}})$
- for $n = 1, \ldots, N$ do
- end for
実装
$K = 3$の2次元での結果を可視化するとこのような結果になりました.