ガウス混合モデルで変分推論
\begin{align} \newcommand{\b}[1]{\mathbf{#1}} \newcommand{\bo}[1]{\boldsymbol{#1}} \nonumber \end{align}
ベイズ推論による機械学習入門より,ガウス混合モデルで変分推論をしてみます.
次のように,潜在変数とパラメータに分けて近似します.
\begin{align} p(\b{S}, \bo{\mu}, \bo{\Lambda}, \bo{\pi} | \b{X}) = q(\b{S}) q(\bo{\mu}, \bo{\Lambda}, \bo{\pi}) \end{align}
まず$q(\b{S})$について考えていきます.$\b{S}$を含む分布のみに着目すると \begin{align} \ln q(\b{S}) &= \left< \ln p(\b{X}, \b{S}, \bo{\mu}, \bo{\pi}, \bo{\Lambda}) \right>_{q(\bo{\mu}, \bo{\Lambda}, \bo{\pi})} + \mathrm{const.} \newline &= \left< \ln p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) p(\b{S} | \bo{\pi}) p(\bo{\mu}, \bo{\Lambda}) p(\bo{\pi}) \right>_{q(\bo{\mu}, \bo{\Lambda}, \bo{\pi})} + \mathrm{const.} \newline &= \left< \ln p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) \right>_{q(\bo{\mu}, \bo{\Lambda})} + \left< \ln p(\b{S} | \bo{\pi}) \right>_{q(\bo{\pi})} + \mathrm{const.} \newline &= \sum_{n = 1}^N \left\{ \left< \ln p(\b{x}_n | \b{s}_n, \bo{\mu}, \bo{\Lambda}) \right>_{q(\bo{\mu}, \bo{\Lambda})} + \left< \ln p(\b{s}_n | \bo{\pi}) \right>_{q(\bo{\pi})} \right\} + \mathrm{const.} \end{align}
各項をそれぞれ見ていきます.
\begin{align} & \left< \ln p(\b{x}_n | \b{s}_n, \bo{\mu}, \bo{\Lambda}) \right>_{q(\bo{\mu}, \bo{\Lambda})} \newline &= \sum_{k = 1}^K \left< s_{n, k} \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} + \mathrm{const.} \newline &= \sum_{k = 1}^K \left< s_{n, k} \left\{ - \frac{1}{2} (\b{x}_n - \bo{\mu}_k)^T \bo{\Lambda}_k (\b{x}_n - \bo{\mu}_k) + \frac{1}{2} \ln |\bo{\Lambda}_k| \right\} \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} + \mathrm{const.} \newline &= \sum_{k = 1}^K \left< s_{n, k} \left\{ - \frac{1}{2} \b{x}_n^T \bo{\Lambda}_k \b{x}_n + \b{x}_n^T \bo{\Lambda}_k \bo{\mu}_k - \frac{1}{2} \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k + \frac{1}{2} \ln |\bo{\Lambda}_k| \right\} \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} + \mathrm{const.} \newline &= \sum_{k = 1}^K s_{n, k} \left\{ - \frac{1}{2} \b{x}_n^T \left< \bo{\Lambda}_k \right> \b{x}_n + \b{x}_n^T \left< \bo{\Lambda}_k \bo{\mu}_k \right> - \frac{1}{2} \left< \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k \right> + \frac{1}{2} \left< \ln |\bo{\Lambda}_k| \right> \right\} + \mathrm{const.} \end{align}
\begin{align} \left< \ln p(\b{s}_n | \bo{\pi}) \right>_{q(\bo{\pi})} = \left< \ln \mathrm{Cat} (\b{s}_n | \bo{\pi}) \right>_{q(\bo{\pi})} = \sum_{k = 1}^K s_{n, k} \left< \ln \pi_k \right> \end{align}
よって
\begin{align} q(\b{s}_n) = \mathrm{Cat} (\b{s}_n | \bo{\eta}_n) \end{align}
\begin{align} \eta_{n, k} \propto \exp \left\{ - \frac{1}{2} \b{x}_n^T \left< \bo{\Lambda}_k \right> \b{x}_n + \b{x}_n^T \left< \bo{\Lambda}_k \bo{\mu}_k \right> - \frac{1}{2} \left< \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k \right> + \frac{1}{2} \left< \ln |\bo{\Lambda}_k| \right> + \left< \ln \pi_k \right> \right\} \quad \left( \mathrm{s.t.} \; \sum_{k = 1}^K \eta_{n, k} = 1 \right) \end{align}
次は$q(\bo{\mu}, \bo{\Lambda}, \bo{\pi})$です. \begin{align} \ln q(\b{S}) &= \left< \ln p(\b{X}, \b{S}, \bo{\mu}, \bo{\pi}, \bo{\Lambda}) \right>_{q(\b{S})} + \mathrm{const.} \newline &= \left< \ln p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) p(\b{S} | \bo{\pi}) p(\bo{\mu}, \bo{\Lambda}) p(\bo{\pi}) \right>_{q(\b{S})} + \mathrm{const.} \newline &= \left< \ln p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) \right>_{q(\b{S})} + \ln p(\bo{\mu}, \bo{\Lambda}) + \left< \ln p(\b{S} | \bo{\pi}) \right>_{q(\b{S})} + \ln p(\bo{\pi}) + \mathrm{const.} \end{align}
この変形によって,$\bo{\mu}, \bo{\Lambda}$と$\bo{\pi}$の2つの分布に分けることができることが分かります. $q(\bo{\mu}, \bo{\Lambda})$の方から見ていきます.
\begin{align} \ln q(\bo{\mu}, \bo{\Lambda}) &= \left< \ln p(\b{X} | \b{S}, \bo{\mu}, \bo{\Lambda}) \right>_{q(\b{S})} + \ln p(\bo{\mu}, \bo{\Lambda}) + \mathrm{const.} \newline &= \sum_{n = 1}^N \left< \sum_{k = 1}^K \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) \right>_{q(\b{s}_n)} + \sum_{k = 1}^K \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) + \mathrm{const.} \newline &= \sum_{k = 1}^K \left\{ \sum_{n = 1}^N \left< s_{n, k} \right> \ln \mathcal{N} (\b{x}_n | \bo{\mu}_k, \bo{\Lambda}_k^{-1}) + \ln \mathrm{NW} (\bo{\mu}_k, \bo{\Lambda}_k | \b{m}, \beta, \nu, \b{W}) \right\} + \mathrm{const.} \end{align}
このことから,$K$個の分布に分解できることが分かります.つまり$q(\bo{\mu}, \bo{\Lambda}) = \prod_{k = 1}^K q(\bo{\mu}_k, \bo{\Lambda}_k)$とできます. $q(\bo{\mu}_k, \bo{\Lambda}_k)$について計算していきます.
ここで,中かっこの内部は前回のギブスサンプリングでの計算と同様の手順で求めることができます.これにより,$q(\bo{\mu}_k | \bo{\Lambda}_k), q(\bo{\Lambda}_k)$がそれぞれガウス分布とウィシャート分布になることが分かります.
\begin{align} \ln q(\bo{\mu}_k | \bo{\Lambda}_k) = - \frac{1}{2} \left\{ \bo{\mu}_k^T \left( \sum_{n = 1}^N \left< s_{n, k} \right> + \beta \right) \bo{\Lambda}_k \bo{\mu}_k - 2 \bo{\mu}_k^T \left( \bo{\Lambda}_k \sum_{n = 1}^N \left< s_{n, k} \right> \b{x}_n + \beta \bo{\Lambda}_k \b{m} \right) \right\} \end{align}
\begin{align} q(\bo{\mu}_k | \bo{\Lambda}_k) = \mathcal{N} (\bo{\mu}_k | \hat{\b{m}}_k, (\hat{\beta}_k \bo{\Lambda}_k)^{-1}) \end{align}
\begin{align} \hat{\beta}_k = \sum_{n = 1}^N \left< s_{n, k} \right> + \beta, \hat{\b{m}}_k = \frac{ \sum_{n = 1}^N \left< s_{n, k} \right> \b{x}_n + \beta \b{m} }{\hat{\beta}_k} \end{align}
\begin{align} \ln q(\bo{\Lambda}_k) = \frac{ \sum_{n = 1}^N \left< s_{n, k} \right> + \nu - D - 1 }{2} \ln |\bo{\Lambda}_k| - \frac{1}{2} \mathrm{Tr} \left[ \left( \sum_{n = 1}^N \left< s_{n, k} \right> \b{x}_n \b{x}_n^T + \beta \b{m} \b{m}^T - \hat{\beta}_k \hat{\b{m}}_k \hat{\b{m}}_k^T + \b{W}^{-1} \right) \bo{\Lambda}_k \right] + \mathrm{const.} \end{align}
\begin{align} q(\bo{\Lambda}_k) = \mathrm{W} (\bo{\Lambda}_k | \hat{\nu}_k, \hat{\b{W}}_k) \end{align}
\begin{align} \hat{\b{W}}_k^{-1} &= \sum_{n = 1}^N \left< s_{n, k} \right> \b{x}_n \b{x}_n^T + \beta \b{m} \b{m}^T - \hat{\beta}_k \hat{\b{m}}_k \hat{\b{m}}_k^T + \b{W}^{-1} \newline \hat{\nu}_k &= \sum_{n = 1}^N \left< s_{n, k} \right> + \nu \end{align}
最後に$q(\bo{\pi})$についてですが,これは以前ポアソン混合分布の変分推論の際に求めた結果がそのまま使えます.
\begin{align} q(\bo{\pi}) = \mathrm{Dir} (\bo{\pi} | \hat{\bo{\alpha}}) \end{align}
\begin{align} \hat{\alpha}_k = \sum_{n = 1}^N \left< s_{n, k} \right> + \alpha_k \end{align}
以上より,各確率分布が求まったので,期待値を求めることができます.
\begin{align} \left< s_{n, k} \right> &= \eta_{n, k} \newline \left< \ln | \bo{\Lambda}_k | \right> &= \sum_{d = 1}^D \psi(\frac{\hat{\nu}_k + 1 - d}{2}) + D \ln 2 + \ln |\hat{\b{W}}_k| \newline \left< \bo{\Lambda}_k \bo{\mu}_k \right> &= \hat{\nu}_k \hat{\b{W}}_k \hat{\b{m}} \newline \left< \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k \right> &= \hat{\nu}_k \hat{\b{m}}_k^T \hat{\b{W}}_k \hat{\b{m}}_k + \frac{D}{\hat{\beta}_k} \end{align}
下の2つは以下のような手順によって求めています.
\begin{align} \left< \bo{\Lambda}_k \bo{\mu}_k \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} &= \left< \bo{\Lambda}_k \bo{\mu}_k \right>_{q(\bo{\mu}_k | \bo{\Lambda}_k) q(\bo{\Lambda}_k)} \newline &= \left< \bo{\Lambda}_k \left< \bo{\mu}_k \right>_{q(\bo{\mu}_k | \bo{\Lambda}_k)} \right>_{q(\bo{\Lambda}_k)} \newline &= \left< \bo{\Lambda}_k \hat{\b{m}}_k \right>_{q(\bo{\Lambda}_k)} \newline &= \hat{\nu}_k \hat{\b{W}}_k \hat{\b{m}}_k \end{align}
\begin{align} \left< \bo{\mu}_k^T \bo{\Lambda}_k \bo{\mu}_k \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} &= \mathrm{Tr} \left[ \left< \bo{\mu}_k \bo{\mu}_k^T \bo{\Lambda}_k \right>_{q(\bo{\mu}_k, \bo{\Lambda}_k)} \right] \newline &= \mathrm{Tr} \left[ \left< \left< \bo{\mu}_k \bo{\mu}_k^T \right>_{q(\bo{\mu}_k | \bo{\Lambda}_k)} \bo{\Lambda}_k \right>_{q(\bo{\Lambda}_k)} \right] \newline &= \mathrm{Tr} \left[ \left< \left\{ \hat{\b{m}}_k \hat{\b{m}}_k^T + (\hat{\beta}_k \bo{\Lambda}_k)^{-1} \right\} \bo{\Lambda}_k \right>_{q(\bo{\Lambda}_k)} \right] \newline &= \mathrm{Tr} \left[ \left< \hat{\b{m}}_k \hat{\b{m}}_k^T \bo{\Lambda}_k + \frac{1}{\hat{\beta}_k} \b{I}_D \right>_{q(\bo{\Lambda}_k)} \right] \newline &= \mathrm{Tr} \left[ \hat{\b{m}}_k \hat{\b{m}}_k^T \hat{\nu}_k \hat{\b{W}}_k + \frac{1}{\hat{\beta}_k} \b{I}_D \right] \newline &= \mathrm{Tr} \left[ \hat{\b{m}}_k \hat{\b{m}}_k^T \hat{\nu}_k \hat{\b{W}}_k \right] + \frac{1}{\hat{\beta}_k} \mathrm{Tr} \left[ \b{I}_D \right] \newline &= \hat{\nu}_k \hat{\b{m}}_k^T \hat{\b{W}}_k \hat{\b{m}}_k + \frac{D}{\hat{\beta}_k} \end{align}
実装
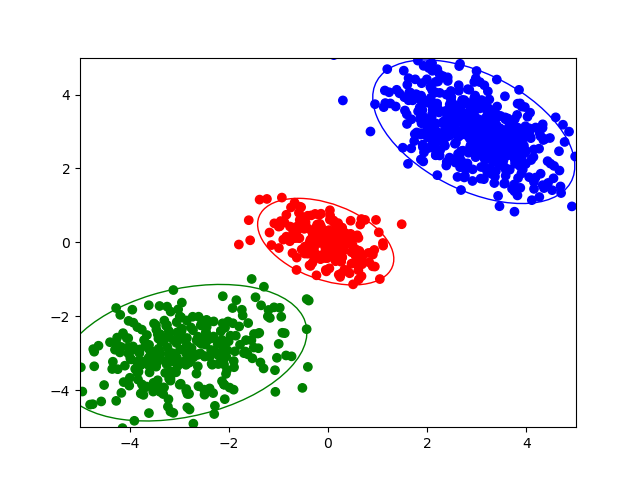
$K = 3, D = 2$の結果を可視化するとこのような結果になりました.