ロジスティック回帰で変分推論
\begin{align} \newcommand{\b}[1]{\mathbf{#1}} \newcommand{\bo}[1]{\boldsymbol{#1}} \nonumber \newcommand{\bs}{\backslash} \end{align}
ベイズ推論による機械学習入門より,ロジスティック回帰で変分推論をしていきます.これは5.6節の内容です.
今回は変分推論の手順のほとんどが書籍の内容をそのままなぞるだけになってしまうので,それらは省略します.記号表記は書籍に合わせているので,書籍を参照してください.
変分推論
変分推論を行うにあたって,cross entropy lossの微分が必要になるため,この導出をします.記号が煩雑になってしまうので,一時的に以下のように$\bo{\alpha}, \bo{\beta}$をおきます.
\begin{align} \bo{\beta} &= \tilde{\b{W}}^T \b{x}_n \newline \bo{\alpha} &= \mathrm{SM} ( \tilde{\b{W}}^T \b{x}_n ) = \mathrm{SM} ( \bo{\beta} ) \end{align}
事前に,softmaxの微分を求めておきます.
\begin{align} \frac{\partial \alpha_u}{\partial \beta_d} = \frac{\partial}{\partial \beta_d} \mathrm{SM}_u (\bo{\beta}) = \frac{\partial}{\partial \beta_d} \left( \frac{\exp(\beta_u)}{\sum_{v = 1}^V \exp(\beta_v) } \right) \end{align}
分母は$v = d$となる$v$が存在するため,$\beta_d$で微分する際に考慮する必要があります.一方,分子は$u \neq d$の場合は$\beta_d$で微分するときは定数とみなすことになるため,微分の対象になりません.よって$u \neq d$の場合と$u = d$の場合に分けて考えていきます.
$u \neq d$の場合
\begin{align} \frac{\partial}{\partial \beta_d} \left( \frac{\exp(\beta_u)}{\sum_{v = 1}^V \exp(\beta_v) } \right) &= - \frac{\exp(\beta_u)}{\left\{ \sum_{v = 1}^V \exp(\beta_v) \right\}^2 } \frac{\partial}{\partial \beta_d} \left( \sum_{v = 1}^V \exp(\beta_v) \right) = - \frac{\exp(\beta_u)}{\left\{ \sum_{v = 1}^V \exp(\beta_v) \right\}^2 } \exp (\beta_d) \newline &= - \frac{\exp(\beta_u)}{ \sum_{v = 1}^V \exp(\beta_v) } \cdot - \frac{\exp(\beta_d)}{ \sum_{v = 1}^V \exp(\beta_v) } = - \mathrm{SM}_u (\bo{\beta}) \mathrm{SM}_d (\bo{\beta}) \end{align}
$u = d$の場合
\begin{align} \frac{\partial}{\partial \beta_d} \left( \frac{\exp(\beta_d)}{\sum_{v = 1}^V \exp(\beta_v) } \right) &= \frac{\exp(\beta_d) \left( \sum_{v = 1}^V \exp(\beta_v) \right) - \exp(\beta_d) \frac{\partial}{\partial \beta_d} \left( \sum_{v = 1}^V \exp(\beta_v) \right) }{ \left\{ \sum_{v = 1}^V \exp(\beta_v) \right\}^2 } \newline &= \frac{\exp(\beta_d) \left( \sum_{v = 1}^V \exp(\beta_v) \right) - \exp(\beta_d) \exp (\beta_d) }{ \left\{ \sum_{v = 1}^V \exp(\beta_v) \right\}^2 } \newline &= \frac{\exp(\beta_d)}{\sum_{v = 1}^V \exp(\beta_v)} - \frac{ \exp(\beta_d) \exp (\beta_d) }{ \left\{ \sum_{v = 1}^V \exp(\beta_v) \right\}^2 } \newline &= \mathrm{SM}_d (\bo{\beta}) - \mathrm{SM}_d (\bo{\beta}) \mathrm{SM}_d (\bo{\beta}) = \mathrm{SM}_d (\bo{\beta}) \left(1 - \mathrm{SM}_d (\bo{\beta}) \right) \end{align}
となります.結果をまとめると
\begin{align} \frac{\partial \alpha_u}{\partial \beta_d} &= \begin{cases} - \mathrm{SM}_u (\bo{\beta}) \mathrm{SM}_d (\bo{\beta}) & (u \neq d) \newline \mathrm{SM}_d (\bo{\beta}) \left(1 - \mathrm{SM}_d (\bo{\beta}) \right) & (u = d) \end{cases} \newline &= \mathrm{SM}_u (\bo{\beta}) \left( \delta_{u, d} - \mathrm{SM}_d (\bo{\beta}) \right) \newline &= \alpha_u \left( \delta_{u, d} - \alpha_d \right) \end{align}
が得られます.$\delta$はクロネッカーのデルタです.
この結果を踏まえて,cross entropy lossの微分を求めます.
\begin{align} \frac{\partial}{\partial \tilde{w}_{m, d}} \mathrm{E}_n &= \frac{\partial}{\partial \tilde{w}_{m, d}} \left\{ - \ln p(\b{y}_n | \b{x}_n, \tilde{\b{W}}) \right\} = \frac{\partial}{\partial \tilde{w}_{m, d}} \left\{ - \ln \mathrm{Cat} (\b{y}_n | \mathrm{SM} (\tilde{\b{W}}^T \b{x}_n)) \right\} \newline &= \frac{\partial}{\partial \tilde{w}_{m, d}} \left\{ - \ln \mathrm{Cat} (\b{y}_n | \bo{\alpha}) \right\} = \frac{\partial}{\partial \tilde{w}_{m, d}} \left\{ - \sum_{u = 1}^D y_{n, u} \ln \alpha_u \right\} \newline &= - \sum_{u = 1}^D y_{n, u} \frac{\partial}{\partial \alpha_u} \left( \ln \alpha_u \right) \frac{\partial \alpha_u}{\partial \tilde{w}_{m, d}} = - \sum_{u = 1}^D y_{n, u} \frac{1}{\alpha_u} \frac{\partial \alpha_u}{\partial \beta_d} \frac{\partial \beta_d}{\partial \tilde{w}_{m, d}} \newline &= - \sum_{u = 1}^D y_{n, u} \frac{1}{\alpha_u} \alpha_u (\delta_{u, d} - \alpha_d) x_{n, m} = - \sum_{u = 1}^D y_{n, u} (\delta_{u, d} - \alpha_d) x_{n, m} \newline &= x_{n, m} \left\{ - \sum_{u \neq d} y_{n, u} (- \alpha_d) - y_{n, d} (1 - \alpha_d) \right\} = x_{n, m} \left\{ \sum_{u \neq d} y_{n, u} \alpha_d - y_{n, d} + y_{n, d} \alpha_d \right\} \newline &= x_{n, m} \left\{ \alpha_d \underbrace{\left( \sum_{u \neq d} y_{n, u} + y_{n, d} \right)}_{= 1} - y_{n, d} \right\} = x_{n, m} \left( \alpha_d - y_{n, d} \right) \newline &= \left( \mathrm{SM}_d (\tilde{\b{W}}^T \b{x}_n) - y_{n, d} \right) x_{n, m} \end{align}
よって,割ときれいな形になることが分かります.
実装
以上の結果を用いて,実装してみました.
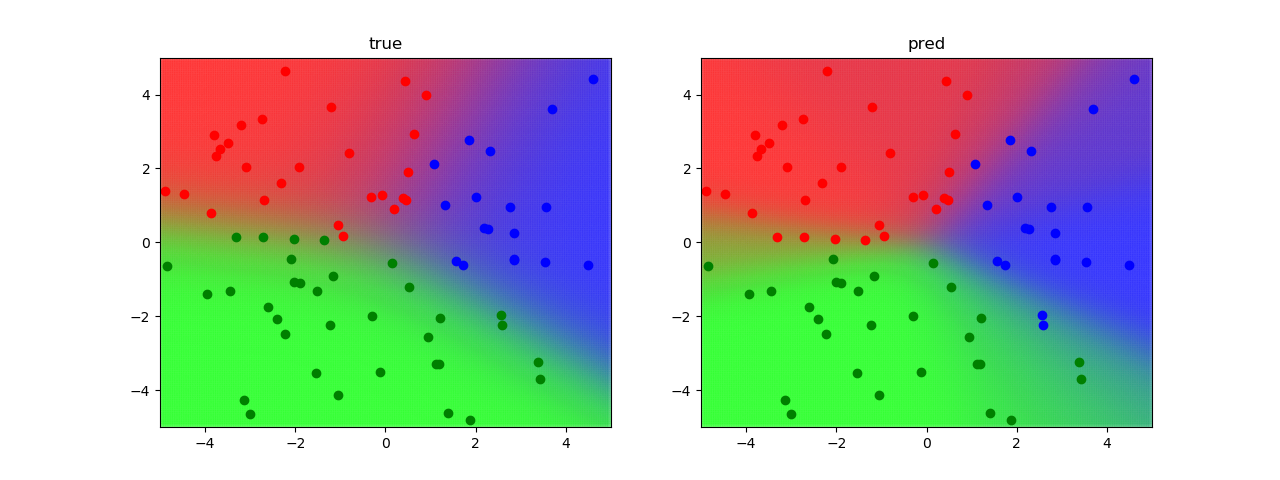
空間上のクラス予測確率を色を用いて可視化しています. 左図は実際のパラメータを用いています.右図は変分推論によって得られたパラメータを用いています.可視化結果から分かるように,変分推論によって上手く実際の分布を近似できていることが分かります.
学習前
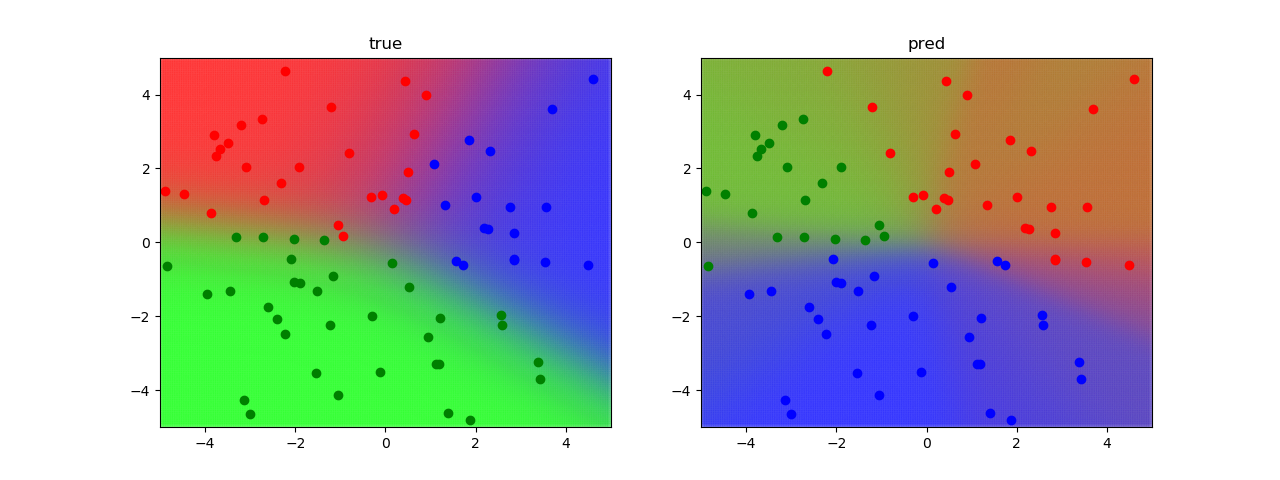
学習後